Часть 2. Операции над нечеткими множествами

Логические операции

Включение.Пусть А и В — нечеткие множества на уни­версальном множестве Е. Говорят, что А содержится в В, если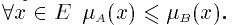 

Обозначение: А ⊂ В.

Иногда используют термин доминирование, т.е. в случае, ко­гда А ⊂ В,говорят, что В доминирует А.

Равенство.А и В равны, если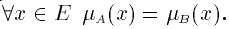 

Обозначение: А = В.

Дополнение.Пусть М = [0, 1], А и В – нечеткие множества, заданные на Е. А и В дополняют друг друга, если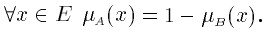 

Обозначение: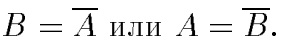 

Очевидно, что 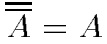 (дополнение определено для М = [0, 1], но очевидно, что его можно определить для любого упорядочен­ного М).

Пересечение. А ⋂ В— наибольшее нечеткое подмножество, содержащееся одновременно в А и В:

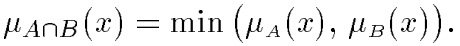
Объединение. A∪В — наименьшее нечеткое подмножество, включающее как А, так и В, с функцией принадлежности:

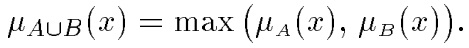
Разность. 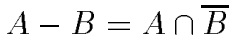 с функцией принадлежности: 

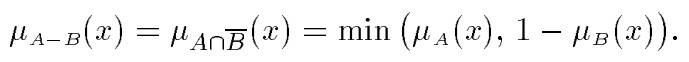
 Дизъюнктивная сумма

А ⊕ В = (A - B) ∪ (B - A) = (A ⋂  ̅B) ∪ (  ̅A ⋂ B)

с функцией принадлежности:

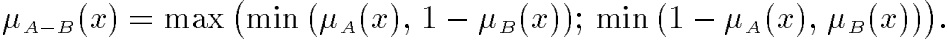
Примеры. Пусть

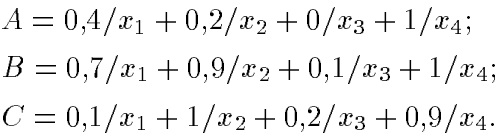
Здесь:

1)          А ⊂ В, т. е. А содержится в Bили Bдоминирует А; С несравнимо ни с A, ни с В, т.е. пары {А, С} и {А, С} — пары недоминируемых нечетких множеств.

2)          A≠ B ≠ C

3)          ̅A = 0,6/x₁ + 0,8/x₂ + 1/x₃ + 0/x₄; ̅B = 0,3/x₁ + 0,1/x₂ + 0,9/x₃ +0/x₄.

4)          А ⋂ В = 0,4/x₁+ 0,2/x₂+ 0/x₃+ 1/х₄.

5)          A ∪ В = 0,7/x₁+ 0,9/x₂+ 0,1/x₃+ 1/x₄.

6)          А - В = А ⋂ ̅В =0,3/x₁+ 0,l/x₂+ 0/x₃+ 0/x₄;

  В - А= ̅А ⋂ В =0,6/x₁+ 0,8/x₂+ 0,l/x₃+ 0/x₄.

7)          А ⊕ В = 0,6/x₁+ 0,8/x₂+ 0,1/x₃+ 0/x₄.

Наглядное представление логических операций над нечеткими множествами. Для нечетких множеств можно строить визуальное представление. Рассмотрим прямоуголь­ную систему координат, на оси ординат которой откладываются значения μ_А(х), на оси абсцисс в произвольном порядке распо­ложены элементы Е (мы уже использовали такое представление в примерах нечетких множеств). Если Е по своей природе упо­рядочено, то этот порядок желательно сохранить в расположении элементов на оси абсцисс. Такое представление делает нагляд­ными простые логические операции над нечеткими множествами (см. рис. 1.3).

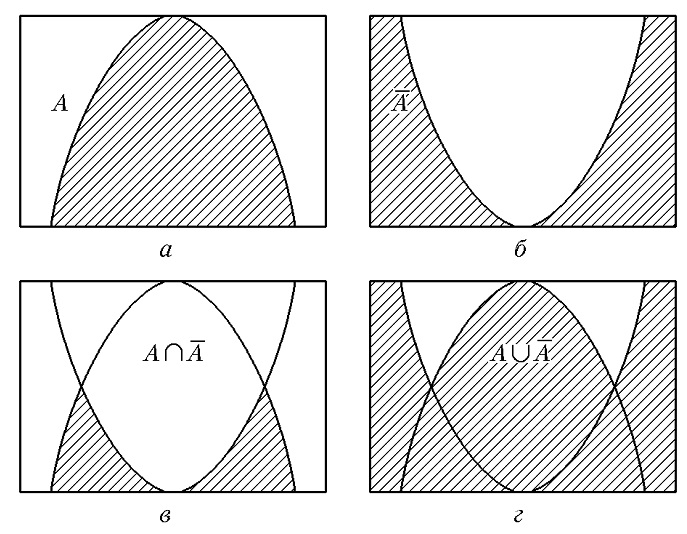
Рис. 1.3. Графическая интерпретация логических операций: α— нечеткое мно­жество А; б — нечеткое множество ̅А, в — А ⋂ ̅А; г— A ∪ ̅А

На рис. 1.3α заштрихованная часть соответствует нечеткому множеству А и, если говорить точно, изображает область значений А и всех нечетких множеств, содержащихся в А. На рис. 1.3б, в, г даны ̅А, А ⋂  ̅A, A U  ̅А.

Свойства операций ∪ и ⋂

Пусть А, В, С — нечеткие множества, тогда выполняются сле­дующие свойства:

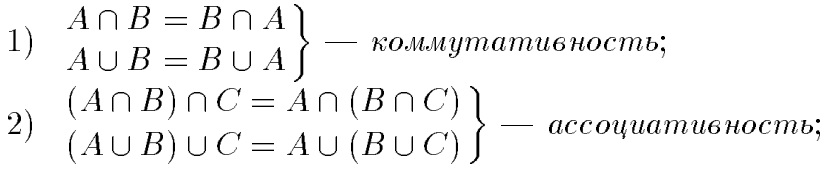
В отличие от четких множеств, для нечетких множеств в общем

случае:

A ⋂ ̅A ≠ ∅, A ∪ ̅A ≠ E

 (что, в частности, проиллюстрировано выше в примере наглядного представления нечетких множеств).

Замечание. Введенные выше операции над нечеткими мно­жествами основаны на использовании операций maxи min. В те­ории нечетких множеств разрабатываются вопросы построения обобщенных, параметризованных операторов пересечения, объеди­нения и дополнения, позволяющих учесть разнообразные смысло­вые оттенки соответствующих им связок «и», «или», «не».

Один из подходов к операторам пересечения и объединения за­ключается в их определении в классе треугольных норм и конорм.

Треугольной нормой(t-нормой) называется двуместная дей­ствительная функция T: [0, 1] x[0, 1] → [0, 1], удовлетворяющая следующим условиям:

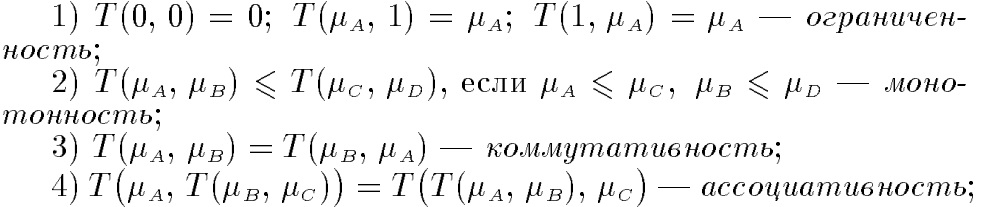
Примеры треугольных норм

min(μ_A, μ_B)

произведение μ_A· μ_B

max(0, μ_A+ μ_B - 1).

Треугольной конормой(t-конормой) называется двуместная действительная функция S: [0, 1] x[0, 1] → [0, 1] со свойствами:

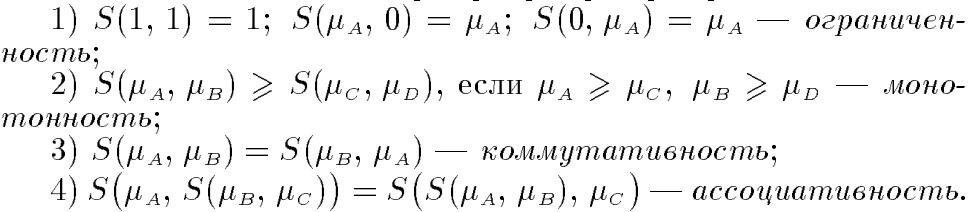
Примеры t-конорм

max(μ_A, μ_B)

μ_A+ μ_B- μ_A· μ_B

min(1, μ_A+ μ_B).

Алгебраические операции над нечеткими множествами

Алгебраическое произведение А иВобозначается A·В и опре­деляется так: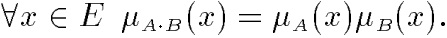 

Алгебраическая суммаэтих множеств обозначается А+ В и определяется так: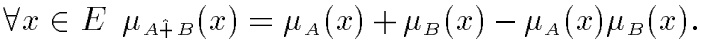 

Для операций {-, +} выполняются свойства:

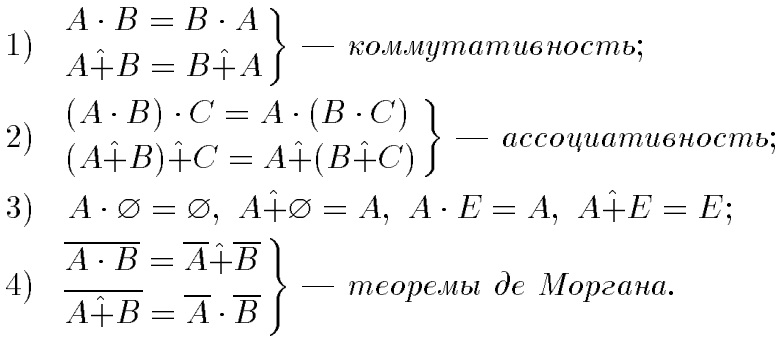
Не выполняются:

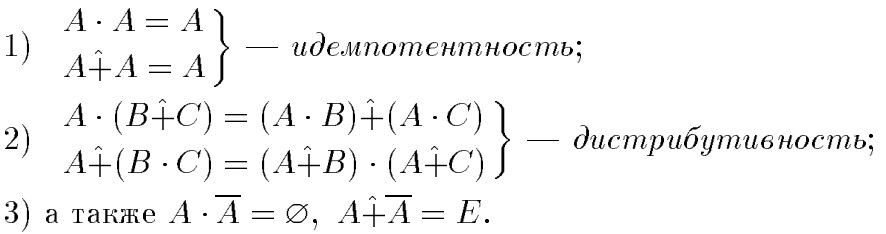
Замечание.При совместном использовании операций { U, ⋂, + , • } выполняются свойства:

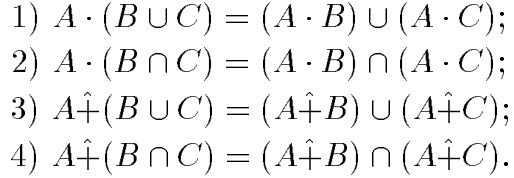
На основе операции алгебраического произведения определя­ется операция возведения в степень α нечеткого множества А, где α— положительное число. Нечеткое множество А^α опреде­ляется функцией принадлежности μ^α_A= μ^α_A(x). Частным случаем возведения в степень являются:

1)          CON(А) = А² — операция концентрирования (уплотне­ния);

2)          DIL(А) = А^0,5 — операция растяжения,

которые используются при работе с лингвистическими неопреде­ленностями (рис. 1.4).

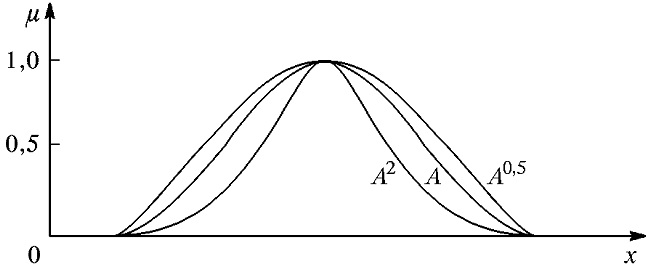
Рис. 1.4. Иллюстрация к понятию операций концентрирования (уплотнения) и растяжения

Умножение на число. Если α — положительное число, такое, что 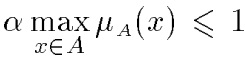, то нечеткое множество αА имеет функцию принадлежности:

μ_αА(х) = αμ_A(x).

Выпуклая комбинация нечетких множеств.Пусть A₁, А₂,..., А_n— нечеткие множества универсального множества Е, aω₁, ω₂, …, ω_n— неотрицательные числа, сумма которых равна 1.

Выпуклой комбинацией A₁, А₂, ..., А_nназывается нечеткое множество А с функцией принадлежности:

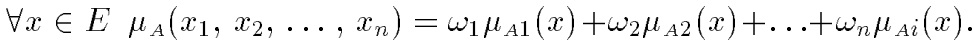
Декартово(прямое) произведение нечетких множеств. Пусть A₁, А₂, ..., А_n— нечеткие подмножества универсальных множеств Е₁, Е₂,…, Е_nсоответственно. Декартово, или прямое произведение А = А₁ x А₂ x... x А_n является нечетким подмно­жеством множества Е = Е₁ x Е₂ x... x Е_n с функцией принад­лежности:

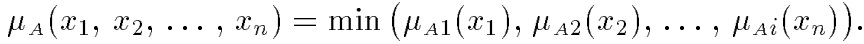
Оператор увеличения нечеткостииспользуется для преобра­зования четких множеств в нечеткие и для увеличения нечеткости нечеткого множества.

Пусть А — нечеткое множество, Е— универсальное множество и для всех хϵЕопределены нечеткие множества К(х).Совокуп­ность всех К(х)называется ядром оператора увеличения нечетко­сти Ф. Результатом действия оператора Ф на нечеткое множество А является нечеткое множество вида

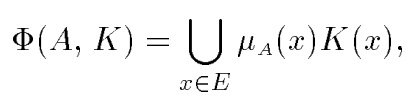
где μ_А(х)К(х) — произведение числа на нечеткое множество.

Пример. Пусть

Е = {1,2,3,4};  А = 0,8/1+ 0,6/2+ 0/3+ 0/4; К(1)=1/1 + 0,4/2;

К(2) = 1/2 + 0,4/1 + 0,4/3; К(3) = 1/3 + 0,5/4; К(4)= 1/4.

Тогда

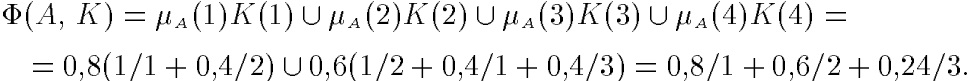
Четкое множество α-уровня(или уровня α). Множеством α-уровня нечеткого множества А универсального множества Е на­зывается четкое подмножество А_α универсального множества Е,определяемое в виде

А_α = { x/μ_A(x) ≥ α },

где α ≤ 1.

Пример. Пусть А = 0,2/x₁+ 0/x₂+ 0,5/x₃+ 1/x₄, тогда A_0,3= { x₃, x₄ }, A_0,7 = { х₄ }.

Достаточно очевидное свойство: если α₁ ≥ 2, то А_α1 ≤ А_α2.